OpenCV与OpenGL中的摄像机投影模型

本文主要分析OpenCV与OpenGL中的摄像机投影模型。

1. OpenCV的摄像机投影模型

投影过程是将三维空间中世界坐标系下的坐标点变换到摄像机坐标系之后，通过归一化Z轴坐标将所有点映射到归一化平面上，自由度由3降为2。摄像机的内参矩阵则建立了归一化平面到图像坐标的对应关系，将坐标原点移到了左上角，并且根据图像的分辨率将连续空间的坐标与离散的像素坐标关联起来。

使用公式来表示OpenCV中的投影过程：

$s\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}\begin{bmatrix}r_{11}&r_{12}&r_{13}&t_1\\r_{21}&r_{22}&r_{23}&t_2\\r_{31}&r_{32}&r_{33}&t_3\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix}$

其中$(X,Y,Z)$为世界坐标系下的三维空间坐标，$(u,v)$为投影后的像素坐标，$(f_x,f_y)$为以像素为单位的焦距，$(c_x,c_y)$为主点，通常在图像中心，$r_{xx}$为旋转矩阵的元素，$t_x$为平移向量，这二者可表示为变换矩阵$[R|t]$。

采用非齐次坐标表达：

$\begin{bmatrix}x\\y\\z\end{bmatrix}=R\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix}+t\\ x'=x/z\\ y'=y/z\\ u=f_x\times x'+c_x\\ v=f_y\times y'+c_y$

2. OpenGL中的摄像机投影模型

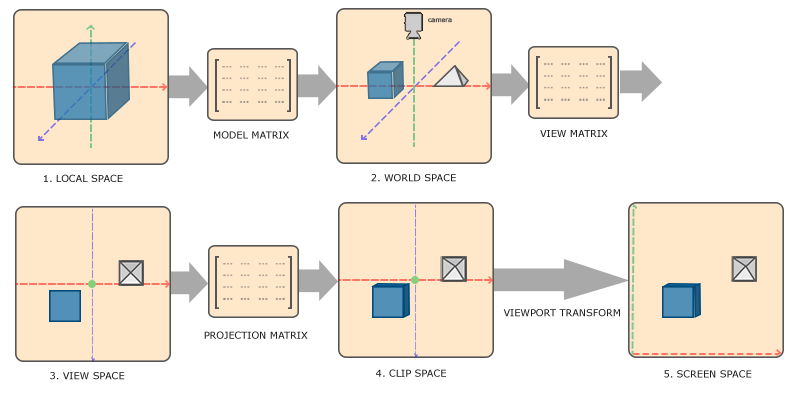
OpenGL中的投影与OpenCV类似，不同之处在于归一化时采用了裁剪空间的设定，只对摄像机前方的一部分区域渲染，其他区域中的内容会舍弃。

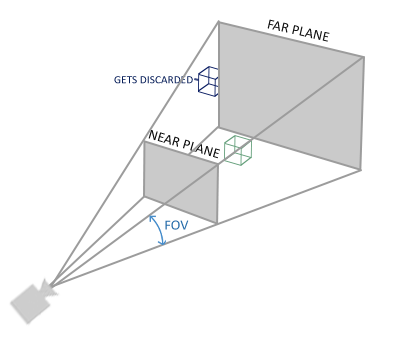
裁剪空间的构成是由摄像机的FOV，以及远、近两个平面围成的，其中FOV在$x,y$两个方向上通常会不同，需要两个数值$fovx$和$fovy$来表示，或者提供FOV和一个宽高比例。

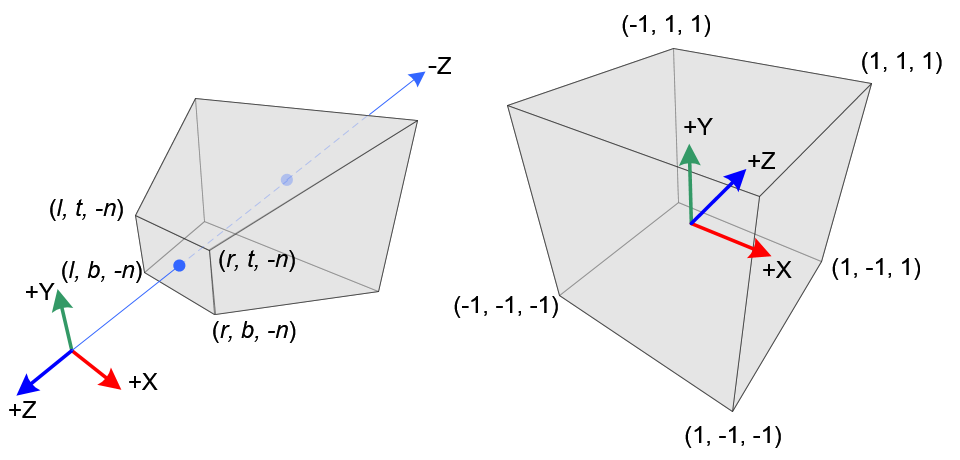
归一化的过程是将裁剪空间的区域映射到一个标准化的坐标空间，该空间是一个立方体，所有顶点的在每个轴上的坐标均为1或-1。变换之后可以比较方便的筛选需要渲染的坐标，也就是判断是否处于立方体内部。

该变换由一个线性变换完成，其表示如下：

$\begin{bmatrix}X_c\\Y_c\\Z_c\\W_c\end{bmatrix}=\begin{bmatrix}\frac{1}{tan(fovx/2)}&0&0&0\\0&\frac{1}{tan(fovy/2)}&0&0\\0&0&-\frac{f+n}{f-n}&-\frac{2fn}{f-n}\\0&0&-1&0\end{bmatrix}\begin{bmatrix}X_e\\Y_e\\Z_e\\1\end{bmatrix}$

其中$f,n$分别代表远、近平面的距离，$(X_e,Y_e,Z_e,1)$为摄像机坐标系下的齐次坐标，$(X_c,Y_c,Z_c,W_c)$为裁剪空间下的齐次坐标，归一化后的结果$(X_n,Y_n,Z_n)=(X_c/W_c,Y_c/W_c,Z_c/W_c)$。

从变换公式来看，有：

$W_c=-Z_e\\ X_n=-\frac{1}{tan(fovx/2)}\frac{X_e}{Z_e}\\ Y_n=-\frac{1}{tan(fovy/2)}\frac{Y_e}{Z_e}$

该表达式与OpenCV中归一化到单位平面的过程有相似之处，除了要乘上一个系数。

从归一化坐标到图像像素坐标的变换与OpenCV中相同，需要放缩和平移。这里先不考虑$Z_n$，因为最终的投影结果是二维的，只与$X_n,Y_n$有关，而$Z_n$的主要用处是判断是否渲染以及判断遮挡。需要注意的是标准化坐标空间的Y轴是朝上的，而OpenCV中的Y轴是朝下的。